그래프 이해해보기

그래프 : 실제 현상이나 사물을 정점과 간선으로 표현한 자료구조이다.

 

노드(Node): 사물의 위치, 정점(Vertex)라고도 한다.

간선(Edge): 노드를 연결하는 선이다.(link ,branch라고도 한다.)

인접 정점: 간선으로 연결된 정점을 말한다.

 

정점의 차수(degree): 무방향 그래프에서 한정점에 연결된 선의 개수라고 보면 된다.

 

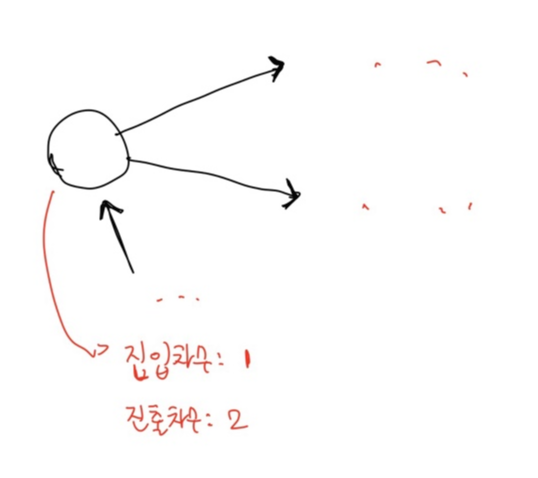
진입차수(in-degree):방향그래프에서 외부에서 한정점으로 들어오는 간선의 개수이다.

진출차수(out-degree):방향그래프에서 외부로 진출하는 간선의 개수이다.

 

 

 

 

경로 길이: 경로 구성을 위해서 사용된 간선의 개수이다.

 

단순 경로 : 처음과 끝정점을 제외하고 중복된 정점이 없는 경로이다.

 

사이클 : 단순경로의 시작과 끝 정점이 같은 그래프이다.

 

 

 

 

 

 

그래프의 종류

 

1.무방향 그래프

 

방향이 없는 그래프

간선을 통해 노드(정점)이 양방향으로 모두 갈 수 있다.

노드A,B가 연결되어 있으면 (A,B) , (B,A)로 표시한다.

 

2.방향 그래프

 

간선에 방향이 있는 그래프다.

A->B로 연결  :  <A,B>로 표기한다.

B->A로 연결  :  <B,A>로 표기한다.

 

 

가중치 그래프 (네트워크)

간선(Edge)에 비용또는 가중치가 할당된 그래프이다.

 

 

연결 그래프

무방향 그래프에 있는 모든 노드들에 대해 항상 경로가 존재하는 경우를 말한다.

-> 모든정점이 어떻게든 하나의 그래프안에서 연결되어 있는 경우

 

 

비연결 그래프

무방향 그래프에서 특정 노드에 대해서 경로가 존재하지 않는 경우이다.

간선이 하나도 없는 동떨어진 정점이 있는 그래프를 말한다.

 

 

사이클

자동차 경주 트랙처럼 단순경로(시작,끝정점 제외 중복된 정점이 없는 그래프)에서

시작과 끝 정점이 동일한 그래프이다.

 

 

 

비순환 그래프

 

사이클이 없는 그래프를 말한다.

완전 그래프

 

모든 정점이 서로 연결되어 있는 그래프이다.

 

 

연결그래프와 차이점이라면

연결그래프는 하나의 그래프안에서 모든 정점이 연결만 되어있으면 되는 최소조건의 느낌이고

완전 그래프는 각각 하나의 정점에 대해서 다른 모든 정점과 간선이 존재해서 전부 이동이 가능한

조건의 느낌이라고 생각한다.

 

트리와 그래프의 차이

트리는 그래프의 특별한 한 종류이다.

 

	그래프	트리
정의	노드와 간선으로 표현된 자료구조	방향성이 있는 비순환 그래프
방향성	방향, 무방향 둘다 존재한다.	방향만 존재한다
사이클	가능하다	X
루트 노드	X	O
부모자식	X	O

 

 

파이썬에서 그래프 표현하기

: 딕셔너리와 리스트 자료구조를 활요해서 그래프를 표현할 수 있다.

'A': ['B', 'C']   A와 연결된 정점은 B,C이다.